ЭКСПЕРИМЕНТ Резистивно-индуктивно-емкостные схемы
Цели
После проведения данного эксперимента Вы сможете рассчитывать и измерять все токи, напряжения и полные сопротивления в последовательных LCR-схемах (резистивно-индуктивно-емкостных схемах).
Необходимые принадлежности
* Осциллограф
* Цифровой мультиметр
* Макетная панель
* Генератор функции
* Источник постоянного напряжения
* Элементы:
одна катушка индуктивности 100 мГн, один конденсатор 0,1 мкФ, один резистор 4700м.
ВВОДНАЯ ЧАСТЬ
Резистивно-индуктивно-емкостная схема (называемая также LCR-схемой или RLC-схемои) скомбинирована из сопротивления, индуктивности и емкости. Всякий раз, когда катушки и конденсаторы комбинируются в схеме переменного тока,. их реактивные сопротивления гасят друг друга.
Вспомните: катушка индуктивности приводит к запаздыванию тока по отношению к приложенному напряжению на 90 градусов; тогда как конденсатор приводит к тому, что ток опережает напряжение на 90 градусов.
Как результат этого катушка индуктивности аннулирует действие конденсатора, так как их действия противоположны. Аналогично в последовательной схеме, состоящей из индуктивности и емкости, компонент с большей величиной реактивного сопротивления подавляет меньшее реактивное сопротивление.
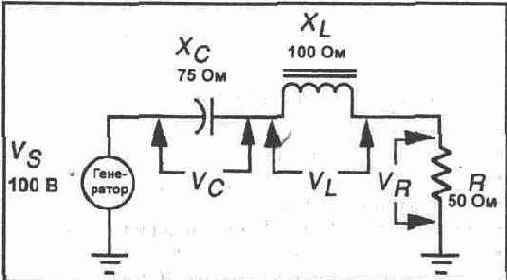
Рис. 21-1.
Пример. В схеме на рисунке 21-1 катушка индуктивности имеет индуктивное сопротивление 100 Ом, а конденсатор имеет емкостное сопротивление 750м, поэтому емкостное сопротивление аннулируется полностью, и поведение схемы будет таким, как будто она обладает общим индуктивным сопротивлением 100 — 75 = 25 Ом. Это
комбинированное общее (эффективное) реактивное сопротивление и используется при расчете полного сопротивления схемы. Поведение схемы имеет индуктивный характер, поскольку XL, больше, чем Хc.
Определение полного сопротивления
Для получения полного сопротивления последовательной резистивно-индуктивно-емкостной схемы используется приведенная ниже формула:
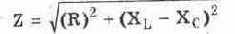
Следовательно, имеем:
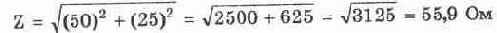
После того, как Вы узнаете полное сопротивление схемы, можно, естественно, рассчитать ток в схеме при помощи закона Ома, в предположении, что известно напряжение источника питания (Vs).
Это выполняется при использовании; следующего выражения с подстановкой найденных выше значений: I=V/Z
I = 100/55,9 = 1,79 А После этого, зная, что ток в каждом компоненте один и тот же, Вы можете определить падения напряжения на каждом, компоненте. Это снова осуществляется при помощи закона Ома и следующих формул: Vс = IR = 1,79(50) = 89,5 В
Vс = IXL = 1,79(100) = 179 В
VL= IXc =1,79(75) = 134,25 В Как и в любой последовательной схеме, значения напряжений распределяются пропорционально значениям активного сопротивления и реактивных сопротивлений: на реактивных сопротивлениях большей величины падают напряжения большей величины. Не забывайте только, что вследствие сдвига фазы, обусловленного типом схемы. Вы не можете попросту складывать непосредственно падения напряжений на компонентах, чтобы получить общее напряжение источника питания. Необходимо при этом выполнять сложение векторных величин. На рисунке 21-2 показано, как это делается при использовании данных предыдущего примера. 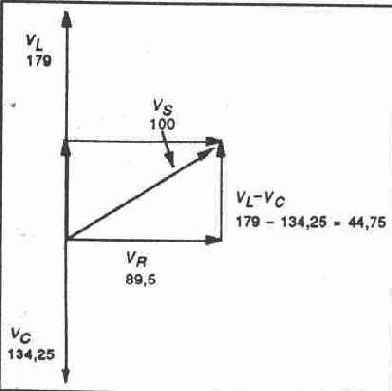
Рис. 21-2.
Краткое содержание В данном эксперименте Вы соберете последовательную резистивно-индуктивно-емкостную схему и сделаете все вычисления, необходимые для расчета схемы. После этого Вы выполните измерения для проверки Ваших расчетов. ПРОЦЕДУРА 1.Измерьте активное сопротивление катушки индуктивности 100 мГн при помощи вашего мультиметра. RL =_____Ом 2. Соберите схему, показанную на рисунке 21-3. Отрегулируйте частоту генератора на 1 кГц и установите величину размаха напряжения на выходе генератора 4 В. 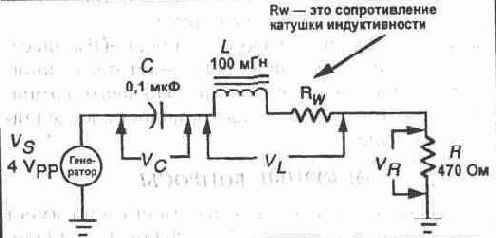
Рис. 21-3. 3. Измерьте Vr, Vl, Vc и Q и запишите полученные значения в таблицу. Напомним, что 9 означает сдвиг фазы тока или V по отношению к приложенному напряжению Vs. 4. Используя табличные данные, вычислите I и Z и запишите их в таблицу. Определите характер схемы (индуктивная или емкостная схема) и отметьте в таблице.

5. Увеличьте частоту генератора до 2 кГц. Сохраняйте величину размаха генератора равной 4 В. 6. Повторите шаги 3 и 4 при этой более высокой частоте. Запишите Ваши данные в таблицу. 7.
Нарисуйте эквивалентные схемы для частоты I кГц и частоты 2 кГц и укажите эквивалентные значения реактивных компонентов в мкФ или в мкГн, как это необходимо. 8. Рассчитайте фактическую мощность (Р), рассеиваемую схемой при каждой частоте, и запишите эти значения в таблицу. Назовите компоненты, которые рассеивают мощность, и сделайте пояснения. ОБЗОРНЫЕ ВОПРОСЫ I. Резистивно-индуктивно-емкостная схема имеет следующие компоненты: XL = 30 Ом, Хc = 42 Ом, R = 150м. Схема в общем является: а) индуктивной, XL = 12 Ом, б) индуктивной, ХL= 72 Ом, в) емкостной, Хc= 72 Ом, г) емкостной, Хc = 12 Ом. 2. В схеме, описанной в вопросе 1, наименьшее падение напряжения на: а) резисторе, б) катушке индуктивности, в) конденсаторе. 3. Каково полное сопротивление (импеданс) схемы, описанной в вопросе I? а) 15 Ом, б) 19,2 Ом, в) 72 Ом, г) 87,5 Ом. 4. Последовательная резистивно-индуктивно-емкостная схема имеет индуктивный характер, если: а) Хc > XL, б) Хc > VL в) VL > Vc, r)XL<Xc. 5. Конденсатор 0,02 мкФ и конденсатор 0,047 мкФ соединены параллельно. Общая эквивалентная емкость равна: а) 0,0094 мкФ, 6)0,014 мкФ, в) 0,0335 мкФ, г) 0,067 мкФ.
