Линейные преобразования уравнений механической характеристики обобщенной машины
Достоинством полученного в §2.2 математического описания процессов электромеханического преобразования энергии является то, что в качестве независимых переменных в нем используются действительные токи обмоток обобщенной машины и действительные напряжения их питания. Такое описание динамики системы дает прямое представление о физических процессах в системе, однако является сложным для анализа.
При решении многих задач значительное упрощение математического описания процессов электромеханического преобразования энергии достигается путем линейных преобразований исходной системы уравнений, при этом осуществляется замена действительных переменных новыми переменными при условии сохранения адекватности математического описания физическому объекту. Условие адекватности обычно формулируется в виде требования инвариантности мощности при преобразовании уравнений. Вновь вводимые переменные могут быть либо действительными, либо комплексными величинами, связанными с реальными переменными формулами преобразования, вид которых должен обеспечивать выполнение условия инвариантности мощности.
Целью преобразования всегда является то или иное упрощение исходного математического описания динамических процессов: устранение зависимости индуктивностей и взаимных индуктивностей обмоток от угла поворота ротора, возможность оперировать не синусоидально меняющимися переменными, а их амплитудами и т. п.

На рис.2.3 обмоточные переменные обозначены в общем виде буквой х с соответствующим индексом, отражающим принадлежность данной переменной к определенной оси координат, и показано взаимное положение в текущий момент времени осей a, b, жестко связанных со статором, осей d, q, жестко связанных с ротором, и произвольной системы ортогональных координат u, v вращающихся относительно неподвижного статора со скоростью wк. Полагаются заданными реальные переменные в осях a, b (статор) и d, q (ротор), соответствующие им новые переменные в системе координат и, v можно определить как суммы проекций реальных переменных на новые оси.
Для большей наглядности графические построения, необходимые для получения формул преобразования, представлены на рис.2.3,а и б для статора и ротора отдельно. На рис.2.3,а показаны оси a, b, связанные с обмотками неподвижного статора, и оси и, v повернутые относительно статора на угол fк=wкt. Составляющие вектора х1u определены как проекции векторов х1a и x1b на ось u, составляющие вектора х1v- как проекции тех же векторов на ось v. Просуммировав проекции по осям, получим формулы прямого преобразования для статорных переменных в следующем виде:

Аналогичные построения для роторных переменных представлены на рис.2.3,б. Здесь показаны неподвижные оси a, b, повернутые относительно них на угол fэл оси d, q, связанные с ротором машины, повернутые относительно роторных осей d и q на угол фк-фэл оси u, v, вращающиеся со скоростью wк и совпадающие в каждый момент времени с осями и, v на рис.2.3,а. Сравнивая рис.2.3,б с рис.2.3,a, можно установить, что проекции векторов x2d и x2q на и, v аналогичны проекциям статорных переменных, но в функции угла (fк-fэл). Следовательно, для роторных переменных формулы преобразования имеют вид

Для пояснения геометрического смысла линейных преобразований, осуществляемых по (2.15) и (2.16), на рис.2.3 выполнены дополнительные построения. Они показывают, что в основе преобразования лежит представление переменных обобщенной машины в виде векторов


Как реальные переменные х1a и х1b, так и преобразованные x1u и х1v являются проекциями на соответствующие оси одного и того же результирующего вектора

При необходимости перехода от преобразованных переменных x1u, x1v, x2u, x2v к реальным переменным обобщенной машины x1a, x1b, x2d, x2q используются формулы обратного преобразова-ния. Их можно получить с помощью построений, выполненных на рис.2.4,а и б аналогично построениям на рис.2.3,а и б:
 |

Формулы прямого (2.15), (2.16) и обратного (2.17) преобразований координат обобщенной машины используются при построении управляющих вычислительных устройств для регулируемых электроприводов переменного тока, а также при проведении исследований, требующих более полного описания процессов в машине, чем достигаемое использованием уравнений механической характеристики обобщенной машины (2.14). Во всех случаях, когда применимы уравнения (2.14), можно непосредственно пользоваться преобразованными уравнениями механической характеристики и выражениями потокосцеплений. Для получения преобразованных уравнений (2.4) и (2.12) необходимо произвести в них замену реальных переменных с помощью формул (2.17) и выполнить преобразования полученных выражений для разделения уравнений по осям и, v.
Эти преобразования несложны, но громоздки, поэтому для пояснения их сути ограничимся преобразованием уравнений электрического равновесия для цепи статора. Подставив выражения переменных (2.17) в первые два уравнения системы (2.2), получим

Уравнения (2.18) содержат переменные разных осей, поэтому для выделения уравнений электрического равновесия, соответствующих обмотке каждой оси, необходимы их преобразования. С этой целью выполним предусмотренные (2.18) операции дифференцирования произведений потокосцеплений на тригонометрические функции угла фк, домножим первое уравнение на cos фк, а второе на sin фк и произведем сложение полученных уравнений. Так как cos2 фк + sin2 фк=1, после приведения подобных членов получим уравнение электрического равновесия для оси и.
Затем домножим первое уравнение (2.18) на - sin фк, а второе на cos фк после выполнения перечисленных операций получим аналогичное уравнение для оси v. В результате таких же преобразований уравнений электрического равновесия для роторных цепей получим преобразованные к осям и, v уравнения электромеханической характеристики обобщенной машины:

где wк=dfк/dt, wэл=dfэл/dt.

Аналогично с помощью (2.17) можно получить преобразованные уравнения потокосцеплений (2.4). Однако их можно достаточно просто записать на основе физических соображений. Переход к осям и, v соответствует переходу к взаимно неподвижным обмоткам, вращающимся со скоростью wк (рис.2.5). Рассматривая этот рисунок, можно определить искомые соотношения:
Таким образом, потокосцепление каждой обмотки в системе координат и, v определяется собственной индуктивностью L1 или L2 и взаимной индуктивностью L12 с другой обмоткой, расположенной на той же оси. Взаимодействие с токами других обмоток отсутствует, так как их

С помощью уравнений (2.20) можно при необходимости в уравнениях электромеханической характеристики (2.19) исключить потокосцепления, выразив их через токи обмоток.
Проверим, выполняется ли при данном координатном преобразовании уравнений обобщенной машины требование инвариантности мощности. Для упрощения записи примем u2d=u2q=0. Тогда вся мощность поступает в машину со стороны статора:

Произведем в (2.21) замену переменных с помощью формул (2.17) и получим

Таким образом, условие инвариантности мощности при рассмотренном преобразовании переменных выполняется. Воспользуемся формулами преобразования для получения удобных для использования выражений электромагнитного момента двигателя. Для неявнополюсной машины уравнение момента получим, заменив в (2.11) реальные переменные на преобразованные по формулам (2.17):

В результате преобразований (2.22) с учетом (2.20) можно получить следующие формулы для определения электромагнитного момента обобщенной машины:

В справедливости формул (2.23) и (2.24) можно убедиться, выразив с помощью (2.20) потокосцепления через токи. Таким путем после преобразований все эти формулы приводятся к полученной выше формуле (2.22).
Объединив уравнения электромеханической характеристики (2.19) с уравнением электромагнитного момента (2.22), получим математическое описание механических характеристик двигателя в осях и, v:

Рассматривая эти уравнения, можно убедиться, что переход к модели со взаимно неподвижными обмотками существенно упрощает математическое описание динамических процессов электромеханического преобразования энергии. Коэффициенты взаимной индукции и потокосцепления взаимно неподвижных обмоток (2.20) становятся независимыми от механической координаты, а движение реальных обмоток и вращение координатных осей учитываются в уравнениях электрического равновесия введением дополнительных ЭДС вращения. Значительно упрощается уравнение электромагнитного момента двигателя, в котором устраняется непосредственная зависимость от угла фэл и электромеханическая связь проявляется посредством зависимости токов и потокосцеплений обмоток от скорости двигателя.
Построения на рис.2.3 свидетельствуют о возможности представления переменных обобщенной машины в комплексной форме и перехода к записи уравнений относительно результирующих векторов. Напряжения, токи, потокосцепления в (2.19) и (2.22) являются проекциями результирующих векторов, изображающих соответствующие величины, на ортогональные оси координат и, v. Если ось и принять за действительную, а ось v - за мнимую ось плоскости комплексного переменного, то изображающие векторы можно представить в виде

Уравнения (2.19) при комплексной записи изображающих векторов для оси и представляют собой действительную часть соответствующих комплексных уравнений статора и ротора, а для оси v - мнимую. Этому условию отвечают следующие уравнения динамической механической характеристики в комплексной форме:

где i*2 - величина, комплексно-сопряженная величине i2.
Векторы потокосцеплений могут быть выражены через результирующие векторы токов статора i1 и ротора i2:

Подставив (2.28) в (2.27), получим уравнения механической характеристики, выраженные через векторы результирующих токов статора и ротора:

где р=d/dt.
Комплексное преобразование при wэл=const дает возможность аналитическим путем исследовать зависимость момента машины от времени при электромагнитном переходном процессе и в дальнейшем изложении будет для этой цели использовано.
Рассмотренные вещественное и комплексное преобразования уравнений механической характеристики обобщенной машины в значительной степени облегчают анализ динамических режимов электропривода и во многих случаях позволяют при моделировании на ЭВМ вместо реальных переменных токов и напряжений обмоток оперировать соответствующими им после преобразования постоянными величинами. Этого в ряде случаев удается достигнуть удачным выбором угловой скорости координатных осей u, v. На практике широко используются следующие варианты выбора этой скорости.
Выбор wк=0 обеспечивает преобразование реальных переменных ротора, выраженных в осях d, q к неподвижным осям a, b, связанным со статором машины. Уравнения электромеханической характеристики в осях а, Р имеют вид

При преобразовании а, р напряжения и токи обмоток машины остаются переменными, но имеют одинаковую частоту, равную частоте тока статора.
Выбор wк=wэл соответствует преобразованию реальных переменных машины к осям d, q, жестко связанным с ротором машины. Уравнения электромеханической характеристики в осях d, q принимают вид

Здесь также напряжения и токи являются переменными, но имеют как в роторной, так и в статорной обмотках частоту w2эл=w0-wэл т.е. частоту тока ротора. В синхронных машинах в статических режимах работы w0эл=wэл, поэтому использование уравнений (2.31) позволяет оперировать соотношениями, аналогичными постоянному току, как показано для следующего варианта.
Если положить wк=w0эл, можно осуществить преобразование х, у - выражение всех переменных системы в осях х, у, вращающихся с синхронной скоростью поля машины, при этом уравнения электромеханической характеристики записываются так:

Пусть при этом к реальным обмоткам статора приложена симметричная двухфазная система напряжений:
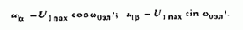
С помощью формул прямого преобразования (2.15), положив wк=w0эл и фк=w0эл·t, преобразуем напряжения u1a, u1b в соответствующие им напряжения u1y, u1x:

Таким образом, в синхронно вращающихся осях х, у реальные переменные напряжения, приложенные к обмоткам статора, при принятой начальной фазе преобразуются в постоянное напряжение U1max=const, приложенное к обмотке, расположенной по оси х. Этот результат имеет физический смысл: вращающееся магнитное поле, создаваемое при неподвижных обмотках статора токами, вызванными напряжениями u1а, u1р, при переходе к обмоткам, вращающимся со скоростью поля, может быть создано постоянным напряжением U1max Во многих случаях при исследованиях динамики машин переменного тока возможность замены синусоидальных переменных постоянными, достигаемая преобразованием к соответствующим осям координат, существенно упрощает моделирование и анализ его результатов.
