Математическое описание и структурные схемы разомкнутых электромеханических систем

Электромеханическая связь объединяет электрическую часть электропривода с механической частью в единую электромеханическую систему, математическое описание которой составляют полученные в гл. 1 уравнения движения электропривода вместе с уравнениями механических характеристик электромеханических преобразователей, рассмотренными в гл. 3. В качестве основного представления механической части примем обобщенную двухмассовую расчетную механическую систему (см. рис.1.2,б), частным случаем которой при с12=¥ является жесткое приведенное механическое звено электропривода (см. рис.1.2,в).

Электромеханическая схема электропривода постоянного тока с двигателем независимого возбуждения представлена на рис.4.1,а. Объединив уравнения (1.40) и (3.40) и положив d/dt=р, получим описание динамических процессов в виде

Соответствующая уравнениям (4.1) структурная схема рассматриваемой электромеханической системы показана на рис.4.1,б. При переменном потоке система (4.1) нелинейна, поэтому для исследования динамических процессов необходимо использование ЭВМ либо линеаризация ее в области малых отклонений от точки статического равновесия. При постоянном потоке система линейна и первые два уравнения приводятся к виду (3.41).

Электромеханическая схема электропривода постоянного тока с двигателем последовательного возбуждения представлена на рис.4.2, а. С помощью (1.40) и (3.50) можно записать уравнения динамики этой системы в виде

На рис.4.2,б представлена структурная схема электромеханической системы с двигателем последовательного возбуждения, которая может быть использована при моделировании ее на АВМ или для подготовки программы для расчета на цифровой ЭВМ. При рассмотрении динамических режимов, в которых отклонения переменных от точки статического равновесия не выходят за пределы допустимой линеаризации нелинейной механической характеристики двигателя, следует пользоваться линеаризованным уравнением динамической механической характеристики (3.60).

Уравнения динамики электромеханической системы с асинхронным двигателем (рис.4.3) могут быть записаны с помощью (3.64) в осях х, у в сочетании с уравнениями движения двухмас-совой упругой системы (1.40):

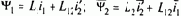где

Необходимость использования для исследования динамики асинхронного электропривода системы (4.3) возникает в случаях, когда рассматриваемый динамический процесс протекает при широких пределах изменения результирующего потока и скорости двигателя (например, пуск двигателя включением на сеть). Как выше отмечалось, во многих практических случаях изучаются динамические процессы, протекающие в окрестности той или иной точки статической характеристики, чаще всего в пределах рабочего участка механической характеристики. При этом целесообразно использовать линеаризованные уравнения динамической механической характеристики асинхронного двигателя (3.95) и (3.111), учитывая вид источника питания.

Математическое описание динамических процессов в синхронном электроприводе получим, записав уравнения механической характеристики в осях d, q, связанных с явнополюсным ротором, на котором размещена обмотка возбуждения, и объединив их с уравнениями движения механической части (1.40):

где

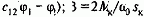
- модуль жесткости для асинхронной составляющей момента, обусловленной действием демпферной обмотки.

Структурная схема синхронного электропривода как объекта управления, справедливая для области рабочего участка асинхронной механической характеристики s<<sk, представлена на рис.4.4. И в данной схеме очевидны существенные нелинейности, обусловленные произведениями переменных и наличием трансцендентных функциональных связей. Поэтому анализ условий движения электропривода с синхронным двигателем, учитывающий основные механические связи и электромагнитные процессы, также требует использования ЭВМ аналогично рассмотренным выше системам постоянного и переменного тока.

Возможности современной вычислительной техники позволяют исследовать динамику конкретных электромеханических систем и при более сложном виде математического описания, чем рассмотренные варианты. В электроприводах переменного тока, управляемых с помощью различных тиристорных преобразователей, в ряде случаев возникает необходимость записи уравнений относительно реальных токов и напряжений фаз трехфазного двигателя.В других случаях дополнительное усложнение математического описания бывает вызвано необходимостью учета несимметрии приложенных к фазам двигателя напряжений, учета зазоров в передачах и других особенностей. Во всех подобных случаях использование ЭВМ помогает получить требуемые решения.

Однако для обобщенного изучения физических особенностей электромеханических систем наиболее эффективным путем является использование допустимых упрощений, позволяющих вести исследование систем аналитическим путем. Приближенные, но удобные для оперативного анализа соотношения имеют неоценимое значение в практике исследования, проектирования и наладки электроприводов. Поэтому в дальнейшем изложении основное внимание уделяется изучению свойств электромеханических систем с учетом влияния нелинейностей на основе линеаризации нелинейных уравнений в окрестности точек статического равновесия.

Содержание раздела

Главная сайта